Tim Robinson

In my last Lisp compiler post, I talked about what I might need to do in order to support tail-recursive calls. I came to the conclusion that my compiler need to start describing the program as a graph of linked basic blocks.

To summarise, a basic block obeys two rules:

• It has a single entry point: the program isn't allowed to branch into the middle of the block
• It has a single exit point: the block always contains a single branch instruction, which appears at the end

For instance, here's a graph of a program that uses a recursive factorial function:

(define (factorial n)
  (if (= n 0) 
    1 
    (* n (factorial (- n 1)))))
(Console.WriteLine (factorial 6))

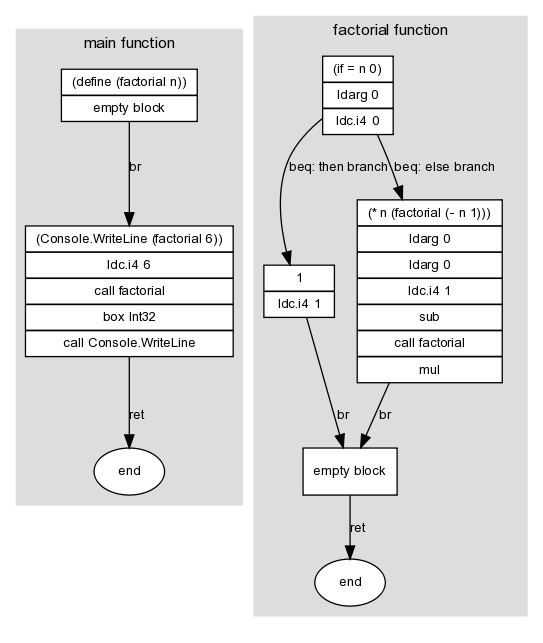
Here I've marked graph edges with a .NET branch instruction (in this case, br, beq or ret). These edges link the graph's nodes -- the basic blocks -- which is where the other instructions in the program appear. A block doesn't need to contain any instructions; for instance, the then and else branches of the if block both lead unconditionally to a single empty block, which in turn exits the function.

To represent the data structures in the graph I added three F# types to the compiler. All of them are immutable apart from ILBlock's Branch field, which I made mutable in order to allow circular references between blocks:

• ILOpCode: a discriminated union with one case for each IL opcode that can appear inside a block -- Add, Box of Type, Call of MethodInfo, etc. Note that call is not considered a branching opcode for these purposes, since it doesn't interrupt the control flow.
• ILBranchOpCode: a discriminated union with one case for each IL opcode that can appear at the end of a block - Beq of ILBlock * ILBlock, Br of ILBlock, Brtrue of ILBlock * ILBlock, NoBranch and Ret. The values for Beq and Brtrue specify both branch possibilities. Each ILBranchOpCode represents an edge in the graph.
• ILBlock: a record containing a list of IlOpCode and a mutable ILBranchOpCode field. Each ILBlock represents a basic block; that is, a node in the graph that can be linked by two or more ILBranchOpCodes.

These new data structures now allow me to split the code concerned with IL generation into two parts: a large function that turns the abstract syntax tree into a graph of basic blocks, and a class that takes this graph and uses it to emit IL code through an ILGenerator. (Actually there are two of these classes -- DynamicMethodTarget and MethodBuilderTarget -- because there is no common base between the two classes .NET provides to instantiate an ILGenerator.)

I won't list out the code in full, since I've submitted it to GitHub (CodeGeneration.fs) and because it's got broadly the same structure as the last time I posted it. The difference is that most of the work is performed by a makeBlock function:

val makeBlock : IILTarget -> Map<string, LispVal> -> LispVal -> Map<string, LispVal> * ILBlock * ILBlock

The purpose of this function is to:

• Accept an IILTarget, an interface capable of defining new methods and local variables; a map, which contains the environment at this point in the program; and a LispVal, which represents one line of code
• Return a new environment, which could be modified version of the one passed in; and two ILBlock instances, which represent the head and tail of a new subgraph

Normally makeBlock will construct only a single block, in which case both the same block object will be returned twice. An if form is more complicated, in that it consists of a diamond shape: the block that contains the code for the test can branch to either the then or the else block, both of which eventually branch back to the same location so that the program can continue. When generating code for an if, makeBlock will return the blocks at the top and bottom of the diamond, ready to be linked together with the rest of the program. (The edges between the then and else blocks are already added.)

Now the the clever part: because we've got the program's structure and code as a graph in memory, we can do some more interesting optimisations. The process of turning this graph into IL goes as follows:

1. Iterate through the graph and assign a IL label to each block. With a depth-first recursive search we have to be careful not to get stuck in a circular reference: to avoid this we keep track of blocks we've already encountered.
2. Iterate through the graph again: generate instructions for each block, followed by an instruction for the block's branch

Take a look at the diagram at the top of this post. Because the diagram doesn't assume a particular ordering of the instructions in memory -- for instance, it doesn't specify whether then or else comes first -- some of its branch instructions are redundant. To generate somewhat sensible IL we have to do some basic optimisations in step (2):

• Case A: If step (1) put two blocks next to each other in memory, we don't need to insert a br instruction between them. Recall that br is an unconditional jump instruction; by leaving it out, we cause the program to fall through from one block to the next.
• Cases B and C: Likewise, use the ordering of the blocks to drop one of the targets of beq and replace it with a fall through
• Case D: If block branches to its target using br, and its target contains no instructions and ends in ret, insert a ret instruction directly

These rules give us a nice opportunity to use pattern matching -- note how the structure of the code is similar to my explanation above:

// Given a list of blocks:
// - branch is the ILBranchOpCode of the first block
// - otherBlocks is a list containing the rest of the blocks
match branch, otherBlocks with
| Br target, next :: _ 
    when target = next -> // Case A
    ()
| Beq (equalTarget, notEqualTarget), next :: _ 
    when equalTarget = next -> // Case B
    generator.Emit(OpCodes.Bne_Un, labels.[notEqualTarget])
| Beq (equalTarget, notEqualTarget), next :: _ 
    when notEqualTarget = next -> // Case C
    generator.Emit(OpCodes.Beq, labels.[equalTarget])
| Br { Instructions = [ ]; Branch = Ret }, _-> // Case D
    generator.Emit(OpCodes.Ret)
| branchOpCode, _ ->    // None of the above apply
    emitBranch labels branchOpCode

Finally -- and here's what I've been building up to with these last couple of posts -- we can implement tail call recursion, using the tail.call prefix. Our graph data structures allow us to literally look for the situation that the IL spec requires: a call instruction immediately followed by ret. In our case, this happens when a block's branch is Ret, and the last instruction of that block is Call:

let rec emitInstructions block = 
    let isRetBlock =
        // A slight hack: due to the above optimisations,
        //  there's a couple of ways of emitting a Ret
        match block with
        | { Branch = Ret } -> true
        | { Branch = Br {
            Instructions = [ ]; 
            Branch = Ret } } -> true
        | _ -> false
    function
    | [ Call _ as instruction ] when isRetBlock ->
        generator.Emit(OpCodes.Tailcall)
        emitInstruction instruction
    | instruction :: otherInstructions ->
        emitInstruction instruction
        emitInstructions block otherInstructions
    | [ ] ->
        ()

By reorganising my compiler to support tail recursion I've learned that:

• Changing your data structures (in this case, implementing a control flow graph) can often make a previously difficult algorithm (tail call detection) straightforward
• If you haven't got any unit tests, you're not refactoring, you're just changing stuff. I've now written unit tests for the main features supported by the compiler. As an aside, I think NUnit tests written in F# look nicer than their C# equivalents, although I was slightly disappointed that NUnit made me write a class with instance methods, whereas it would have been neater to have some functions for test cases defined directly inside an F# module.
• Writing a blog post on a topic before attempting it is a great way to get your thoughts clear in your head before starting

What I might look at next is some more sophisticated algorithms over the control flow graph. Once you have a graph you make available a whole field of algorithms to use on your data. I haven't looked at it yet in detail, but I like Steve Horsfield's data structure for modelling directional graphs.

I'd like to add tail call support to my Lisp compiler. I can think of two approaches to tail recursion:

• Use the .NET tail.call prefix
  • Translate call followed by ret into tail.call followed by ret
  • It's easier to spot this pattern if we put IL in our own data structure before emitting it
  • Our own data structure needs to represent all the IL we use, including labels (for branching) and local variables
  • The label data structure needs a way to represent the target of a branch
  • Note: The tail prefix is a hint that the JIT compiler doesn't have to obey - here's a good explanation of the limitations
• Translate functions that call themselves into loops
  • Our abstract syntax tree doesn't have a way to represent a loop
  • As above, it needs an AST capable of representing branches
  • The F# compiler does this; it's not able to rely on the tail prefix either
  • Can we apply this to functions that call each other recursively? At compile time we might not spot co-recursive functions: F# only allows co-recursive functions if they use the let ... and syntax to define both functions in the same source file.

The ability to represent loops, and control flow in general, seems to be important in your syntax tree. The LLVM approach to this is the basic block:

• One entry point: no branching into the middle of the block
• One exit point: always contains one branch instruction, at the end
• Basic blocks can be connected to form a control flow graph: blocks are vertices, branch instructions are edges
• Control flow graph is: directed (A branches to B); cyclic (A is allowed to branch to A - this is a loop)

How can we represent basic blocks in F#? The intuitive approach means defining a discriminated union:

// An instruction can be a regular opcode, 
//  or a branch to another basic block
type Instruction = CallInstruction of MethodInfo * obj
                 | Branch of BasicBlock

// A basic block is a list of instructions
and BasicBlock = BasicBlock of Instruction list

We have to construct a list of instructions before constructing a basic block. But how do we represent the following?

// C# pseudocode
while (true)
    Console.WriteLine("hello");

// F# abstract syntax tree for the above C#
let instructions =
    [
        Call (writeLine, "hello");

        // How can we branch to something we haven't constructed yet?
        Branch ???
    ]
let program = BasicBlock instructions

The answer is to separate identity of basic blocks from the instructions within them. We could assign names or ids to them. Or, since we're writing F# and not Haskell, we could drop immutability:

// F# abstract syntax tree with mutability - 
//  note property assignment with <-
let program = new BasicBlock()
let instructions =
    [
        Call (writeLine, "hello");
        Branch program
    ]

program.Instructions <- instructions

LLVM does something similar with its C++ API:

// LLVM equivalent in C++

// 'bb' is a basic block within func_main
BasicBlock* label_bb = BasicBlock::Create("bb", func_main, 0);

// First instruction in bb: call puts("hello")
CallInst::Create(func_puts, const_ptr_8, "", label_bb);

// Second instruction in bb: branch back to bb
BranchInst::Create(label_bb, label_bb);

I'm not yet sure of all the implications for my toy compiler, but already I can see some indications about how to structure the code to allow for optimisations like tail calling:

• Structure the entire program as a graph of basic blocks linked by branch instructions
• Abstract syntax trees can't do everything; instead, they appear as instructions within basic blocks
• Construction of basic blocks must be separate from construction of the instructions within them, so that we can refer to a basic block from one of its own instructions
• As it progresses through compiler passes, the program graph starts looking less functional and more imperative, until it eventually represents actual machine instructions
• I should probably read a compiler textbook

This is part 5 of a series of posts on my Lisp compiler written in F#. Previous entries: Introduction, Parsing with fslex and fsyacc, Expression trees and .NET methods, IL generation | Browse the full source of the compiler on GitHub

This post marks the end of the first series of Lisp compiler posts, since we're at the point where the code does something useful while still being compact enough to explain in a few blog posts. In the future it should make an interesting test bed for learning about compiler techniques, which I hope to cover here.

Here's some of the ideas I'd like to try out:

• Implement all the Lisp functionality from Jonathan Tang's Write Yourself a Scheme in 48 Hours tutorial. Jonathan explains how to implement a Scheme interpreter in Haskell, which is a similar goal to my Scheme-like compiler in F#. (It was actually his tutorial that first gave me the idea of doing it in F#.)
• .NET integration:
  • Ability to create new .NET objects, call instance methods, and access properties and events. Currently we're restricted to static methods.
  • Ability to define your own .NET classes. One thing I'd like to be able to do is implement the NUnit tests for this project directly in Lisp, which means the compiler needs to be able to generate instance methods with custom attributes applied.
  • A full System.CodeDom.Compiler implementation: Lisp on ASP.NET anyone?
• Optimisations:

  • Tail call optimisation: replace the call, ret sequence with tail.call, ret. This is less an optmisation and more a necessity, since recursion is currently the only way to implement looping, and we need tail calls to avoid overflowing the stack. The tail opcode prefix is recognised directly by the CLR: another approach would be for the compiler to implement a recursive function as a while loop. Tail calling on .NET is a moderately interesting topic in its own right: see the links from this Stack Overflow question to get an idea of the issues involved.

    Edit: as Paul points out, the trick is to optimise all tail calls, not just tail recursion. It's easy to come up with a pair of functions that call each other: if we just looked for recursive calls back to the same function, we'd blow up the stack in this situation. Luckily for us, the IL tail prefix is valid on any call, as long as it comes just before a ret, so we don't need to be too clever.

  • Arithmetic optimisations: something as simple as simplifying constant expressions at compile time
• A command line compiler, with parameters similar to those of csc.exe or fsc.exe
• Don't generate IL directly to ILGenerator; assemble F# data structures representing the IL, so that we can apply IL optimisations using standard F# constructs such as pattern matching
• Implement flow control within the compiler on top of a flow control graph data structure, along the lines of basic blocks. This will make optimisations of program flow easier to implement.

Let me know if you've found this series useful so far, or if you have any corrections or suggestions on what I've been writing.

This is part 4 of a series of posts on my Lisp compiler written in F#. Previous entries: Introduction, Parsing with fslex and fsyacc, Expression trees and .NET methods | Browse the full source of the compiler on GitHub

What we've done up to this point is:

• Taken a string representing a Lisp program and turned it into an F# data structure representing a list of s-expressions
• Reformatted these s-expressions so we can take some shortcuts when we generate IL
• Written a couple of helper functions that pick the right overload of a .NET method (which our hello world program needs in order to call Console.WriteLine)

In this post I'm going to cover the final step in the compilation process, the generation of the IL itself. By IL, I'm referring to the Common Intermediate Language, the low-level machine-independent opcodes that the .NET JIT compiler turns into native machine code at runtime. The virtual machine on which IL is based operates using a stack for operands and results, rather than the registers that are found on x86 processors. (Using a virtual stack makes IL more portable across CPUs with different register layouts; it's up to the JIT compiler to assign machine registers to stack locations as they're needed.) You can view the IL contained within any .NET assembly using the ildasm tool, which is included with Visual Studio and in the .NET SDK, or within .NET Reflector.

An IL hello world looks like this:

// Push a System.String instance onto the stack. 
// The words "Hello world" are embedded within the executable.
ldstr      "Hello, world"

// Pop one System.Object instance from the stack and call 
// System.Console.WriteLine. This method is declared void, so 
// nothing is pushed onto the stack after the method returns.
call       void [mscorlib]System.Console::WriteLine(object)

// Return to this method's caller
ret

Along with the IL, the assembly -- an EXE or a DLL -- contains various metadata, which describes the types and methods defined within the assembly (such as the Program class and its Main method that contains our code above, and the words "Hello world"), as well as the references the assembly's code makes to the outside world (such as the details of the System.Console.WriteLine method). We don't have to write any of this metadata ourselves, though: the System.Reflection.Emit namespace contains a nice set of types that allow us to construct assemblies, types and methods without worrying about putting together the bytes of the final EXE or DLL file.

We put together the IL itself using the ILGenerator class:

generator.Emit(OpCodes.Ldstr, "Hello world")
generator.Emit(OpCodes.Call, typeof<Console>.GetMethod("WriteLine", [| typeof<obj> |]))
generator.Emit(OpCodes.Ret)

For the purposes of this blog post, we're going to simplify the code generation even further, and use the DynamicMethod class, which allows us to generate a stream of IL opcodes in memory, then execute them, without having to write a full assembly file to disk. (The code on GitHub demonstrates both approaches -- see Compiler.fs for the code that writes an assembly file.)

We're going to write the compile function that I talked about in the last post:

let rec compile
    (generator : ILGenerator)
    (defineMethod : string -> Type -> Type list -> #MethodInfo * ILGenerator)
    (env : Map<string, LispVal>)
    (value : LispVal) 
    : (Map<string, LispVal>)

We'll have given to us: an ILGenerator instance; a function that creates a new method and returns an ILGenerator for that method; a map containing any variables and functions declared earlier on in this function; and a LispVal representing the line of code we're being asked to generate IL for. We'll return a map containing all of the variables and functions originally passed to us, plus any new variables or functions we might have declared in this line of code.

CodeGenerator.fs

let rec compile (generator : ILGenerator) defineMethod =

<code>let f = 
    fun a ->
        fun b ->
            fun c ->
                fun d -> 
                    printfn "called function f with %d %d %d %d" a b c d
</code>

let f a b c d = 
    printfn "called function f with %d %d %d %d" a b c d

let rec compile' env =

So far we've consumed the generator, defineMethod and env parameters. Now we're writing a compile' function, which we're going to use not only when the compile function itself is called, but also recursively from within the compile' function. We do this because we want to be able to generate IL using the same generator and defineMethod parameters originally passed to us, but with different values for env and value.

function
| ArgRef index -> 
    generator.Emit(OpCodes.Ldarg, index)
    env

ArgRef: The compile' function immediately performs pattern matching against its last argument: the F# function keyword acts like fun and match combined. We'll handle each of the LispVal cases in alphabetical order: first is ArgRef, which is a value we'll find within a function's environment. There's one of these for each of the function's parameters, and since IL refers to its arguments using numerical indices, so will we. We use the ldarg opcode to fetch the index'th argument and push it onto the VM stack. We don't change the function's environment, so we return env unchanged.

| Atom a -> 
    a |> ident env |> compile' env

Atom: An atom is a string that refers to a variable or function in the function's environment. We deal with these by calling ident to look up the string in the current environment, then recursively calling compile' to generate the IL for whatever ident finds. In practice this case is only used for variable and function argument lookups; function names are also atoms, but the only thing we do to functions is call them, and we call functions lower down when we encounter an atom within List node. (In a later version we might want to treat function names that appear outside of function calls like C# does, and turn them into delegates.)

| Bool b -> 
    let opCode = 
        if b 
        then OpCodes.Ldc_I4_1 
        else OpCodes.Ldc_I4_0
    generator.Emit opCode
    env

Bool: Bools are the first of our constants to appear. IL represents bools as integers, and it has built-in opcodes whose purpose is to load an integer between 0 and 8 onto the stack, so we generate either ldc.i4.1 for true or ldc.i4.0 for false here. (Our handling of true and false is completely wrong from a Lisp point of view, which uses nil for false and anything else for true.)

let emitIf opCode env thenValue elseValue =
    let thenLabel = generator.DefineLabel()
    let endLabel = generator.DefineLabel()
    generator.Emit(opCode, thenLabel)
    elseValue |> compile' env |> ignore
    generator.Emit(OpCodes.Br, endLabel)
    generator.MarkLabel thenLabel
    thenValue |> compile' env |> ignore
    generator.MarkLabel endLabel

| IfPrimitive (ListPrimitive (Equal, [ a; b ]), thenValue, elseValue) ->
    let env' = a |> compile' env
    let env'' = b |> compile' env'
    emitIf OpCodes.Beq env'' thenValue elseValue
    env''

| IfPrimitive (testValue, thenValue, elseValue) ->
    let env' = testValue |> compile' env
    emitIf OpCodes.Brtrue env' thenValue elseValue
    env'

IfPrimitive: The built-in (if test then else) form. There's a special case for (if (= a b) then else), because IL has its own combined branch-on-equal opcode, beq. If we defined more built-in comparison forms besides Equal, we'd have more special cases here for the other opcodes.

| LambdaDef _ -> 
    raise
        <| new NotImplementedException("didn't expect lambda outside variable")

| LambdaRef _ -> 
    raise <| Compiler("can't compile lambda - try invoking it instead")

LambdaDef, LambdaRef: Here we state two limitations on functions: the first happens if we try to use the (lambda) form outside of a variable declaration, and the second occurs if we try to use a function name outside of a function call, which I mentioned above. In a future version we might want to turn these into .NET delegates, although at the moment we have no way of specifying the delegate type (in fact, we have no way to instantiate instances of .NET objects at all).

| List (Atom a :: args) ->
    match lambdaIdent args env a with
    | LambdaRef (methodInfo, isParamArray, parameterTypes) -> 

List: Here's where we generate .NET method calls, which in Lisp appear as a list, with the function name (an atom) appearing first, followed by the function's arguments, if any. We start by looking up the function name in the environment and expecting it to resolve to a LambdaRef. I talked about the lambdaIdent function in the last post, and it is this function that picks the right method overload given a set of arguments.

        let emitBoxed (expectedType : #Type) env x =
            let env' = compile' env x
            match typeOf env x with
            | a when not expectedType.IsValueType && a.IsValueType -> 
                generator.Emit(OpCodes.Box, a)

            | _ ->
                ()

            env'

A helper function to automatically box instances of value types when needed, so that, for instance, we can pass ints to Console.WriteLine. Note that we need to annotate the F# function signature: expectedType : #Type denotes that expectedType is Type, or one of Type's subclasses. We do this in order to access its IsValueType property.

        let rec emitArgs (parameterTypes : #Type list) env args =
            match args, parameterTypes with
            | arg :: otherArgs, [ parameterType ] when isParamArray ->
                let elementType = parameterType.GetElementType()

                let rec emitArrayInit env position =
                    function
                    | value :: values ->
                        generator.Emit(OpCodes.Dup)
                        generator.Emit(OpCodes.Ldc_I4, int position)
                        let env' = emitBoxed elementType env value
                        generator.Emit(OpCodes.Stelem, elementType)
                        emitArrayInit env' (position + 1) values

                    | [ ] -> 
                        env

                generator.Emit(OpCodes.Ldc_I4, List.length args)
                generator.Emit(OpCodes.Newarr, elementType)
                emitArrayInit env 0 args

            | arg :: otherArgs, parameterType :: otherParameterTypes ->
                emitArgs otherParameterTypes (emitBoxed parameterType env arg) otherArgs

            | [ ], [ ] -> 
                env

            | _ :: _, [ ] -> 
                raise <| new InvalidOperationException(sprintf "got %d too many args" <| List.length args)

            | [ ], _ :: _ -> 
                raise <| new InvalidOperationException(sprintf "got %d too few args" <| List.length parameterTypes)

        let env' = args |> emitArgs parameterTypes env
        generator.Emit(OpCodes.Call, methodInfo)
        env'

The emitArgs helper function emits the IL to put the function's arguments on the stack. For functions that don't take a variable number of arguments we can do this by calling compile' on each node, since compile' leaves the node's value on the VM stack. Calling variable argument functions (again, such as Console.WriteLine) is slightly more intricate, since the last parameter is an array. We use the newarr opcode to instantiate the array, then stelem in a loop to insert arguments into the array one by one.

Since we only deal with static functions at the moment (whether they're .NET methods or our own lambdas) it's safe to use the call opcode in all circumstances. If we were calling instance methods we'd need to be able to call virtual methods using callvirt, and we'd need to automatically box value types when calling interface methods (such as 4.CompareTo(5)) and methods defined on System.Object (such as 4.ToString()). By limiting ourselves to static methods we've avoided these details.

    | v -> raise 
        <| new NotImplementedException(sprintf "can't invoke variable %A" v)

| List (fn :: args) -> 
    raise <| new NotImplementedException(sprintf "can't invoke value %A" fn)

| List [ ] -> 
    raise <| Compiler("can't invoke empty list")

Because we don't know about delegates, we can't call anything other than real functions.

| ListPrimitive (op, args) -> 
    match args with
    | arg :: otherArgs ->
        let opCode = 
            match op with
            | Add -> OpCodes.Add
            | Subtract -> OpCodes.Sub
            | Multiply -> OpCodes.Mul
            | Divide -> OpCodes.Div
            | Equal -> OpCodes.Ceq

        let coerceToInt env x = 
            let env' = compile' env x
            match typeOf env x with
            | t when t = typeof<obj> -> generator.Emit(OpCodes.Call, typeof<Convert>.GetMethod("ToInt32", [| typeof<obj> |]))
            | t when t = typeof<int> -> ()
            | t -> raise <| new NotImplementedException("expected int, got " + t.Name)
            env'

        let emitBinaryOp env arg =
            let env' = coerceToInt env arg
            generator.Emit opCode
            env'

        let env' = coerceToInt env arg
        otherArgs |> List.fold emitBinaryOp env'

    | l -> 
        raise <| Compiler(sprintf "cannot compile list %A" l)

ListPrimitive: The built-in forms for arithmetic and equality are defined as ListPrimitive nodes, and the IL for each of these is fairly similar. Note that our arithmetic operators can handle any number of arguments, and we handle this by pushing the first value onto the VM stack, then using F#'s fold function to apply one of IL's binary operators to each pair. We use Convert.ToInt32 to coerce any strange values to integers. (Note that List.fold is new in the F# May 2009 CTP -- previously this function was called List.fold_left, to match OCaml.)

| Number n -> 
    generator.Emit(OpCodes.Ldc_I4, n)
    env

| String s -> 
    generator.Emit(OpCodes.Ldstr, s)
    env

Number, String: Another couple of constant types: all numbers are integers, and we use the ldc.i4 opcode to push them onto the stack. We saw ldstr in the hello world example at the top of this post.

| VariableDef (name, value) ->
    match value with
    | LambdaDef (paramNames, body) ->
        let (lambdaInfo, lambdaGenerator) = 
            defineMethod
                name
                (typeOf env body)
                (List.replicate (List.length paramNames) (typeof<int>))

        let envWithLambda = 
            env 
            |> (LambdaRef (lambdaInfo, false, (List.map (fun _ -> typeof<int>) paramNames)) 
                |> Map.add name)

        let (envWithLambdaArgs, _) = 
            paramNames 
            |> ((envWithLambda, 0) 
                |> List.fold (fun (env, index) name -> (Map.add name (ArgRef index) env, index + 1)))

        body |> compile lambdaGenerator defineMethod envWithLambdaArgs |> ignore
        lambdaGenerator.Emit(OpCodes.Ret)
        envWithLambda

    | _ ->
        let local = generator.DeclareLocal(typeOf env value)
        let envWithVariable = Map.add name (VariableRef local) env
        compile' envWithVariable value |> ignore
        generator.Emit(OpCodes.Stloc, local)
        envWithVariable

VariableDef: We use VariableDef nodes to declare both functions and variables. There are in fact three possibilities here:

1. (define func (arg1 arg2) body)
2. (define func (lambda (arg1 arg2) body))
3. (define variable value)

The first two cases are treated the same (in fact, the first case is transformed to the second by insertPrimitives, which we saw in the last post), and both of them define a new named function:

1. We call defineMethod to obtain a MethodInfo and an ILGenerator for a new method
2. So that the function can call itself recursively, we insert the function into the environment before we start generating the function's IL. This changed environment is the one that feeds into the next line of code in the function where the declaration appears.
3. We set up a new environment based on the declaring function. This new environment gains a set of ArgRef values that represent the function's arguments.
4. We call compile recursively, with the new ILGenerator that defineMethod gave us

To declare a variable, we first use ILGenerator.DeclareLocal to allocate a new IL local variable, then use the stloc opcode to assign a value to it. As with function declarations, we change the function's environment, and return the changed environment so that it can be fed into the next line of code.

| VariableRef local -> 
    generator.Emit(OpCodes.Ldloc, local)
    env

VariableRef: Last in our alphabetical list of expression tree nodes is VariableRef, which is the node we inserted into the environment just a moment ago to represent local variables. IL gives us the ldloc opcode, which fetches the value from a local variable and places it into the VM stack.

compile'

In the last line of code, we're outside of the compile' definition and back in compile. Recall that we declared compile as a function that accepts two arguments and returns a function that accepts two more: here we're returning that function.

To finish up, let's compile the Lisp code I wrote in the last post, which generates most of the features in our code generator:

(define (fact n) (if (= n 0) 1 (* n (fact (- n 1)))))
(Console.WriteLine "6! = {0}" (fact 6))
(Console.WriteLine "What is your name?")
(Console.WriteLine "Hello, {0}" (Console.ReadLine))

IL disassembly

.class public auto ansi sealed Program
       extends [mscorlib]System.Object
{
  .method public static void  Main() cil managed
  {
    // (Console.WriteLine "6! = {0}" (fact 6))
    IL_0000:  ldstr      "6! = {0}"
    IL_0005:  ldc.i4     0x6
    IL_000a:  call       int32 Program::fact(int32)
    IL_000f:  box        [mscorlib]System.Int32
    IL_0014:  call       void [mscorlib]System.Console::WriteLine(string, object)

    // (Console.WriteLine "What is your name?")
    IL_0019:  ldstr      "What is your name\?"
    IL_001e:  call       void [mscorlib]System.Console::WriteLine(object)

    // (Console.WriteLine "Hello, {0}" (Console.ReadLine))
    IL_0023:  ldstr      "Hello, {0}"
    IL_0028:  call       string [mscorlib]System.Console::ReadLine()
    IL_002d:  call       void [mscorlib]System.Console::WriteLine(string, object)
    IL_0032:  ret
  }

  .method private static int32  fact(int32 A_0) cil managed
  {
    // (if (= n 0) ...
    IL_0000:  ldarg      A_0
    IL_0004:  nop
    IL_0005:  nop
    IL_0006:  ldc.i4     0x0
    IL_000b:  beq        IL_002d

    // else: (* n (fact (- n 1)))
    IL_0010:  ldarg      A_0
    IL_0014:  nop
    IL_0015:  nop
    IL_0016:  ldarg      A_0
    IL_001a:  nop
    IL_001b:  nop
    IL_001c:  ldc.i4     0x1
    IL_0021:  sub
    IL_0022:  call       int32 Program::fact(int32)
    IL_0027:  mul
    IL_0028:  br         IL_0032

    // then: 1
    IL_002d:  ldc.i4     0x1
    IL_0032:  ret
  }
}

And just for fun, using Reflector to disassemble into C#:

C# decompilation

public sealed class Program
{
    private static int fact(int num1)
    {
        return ((num1 == 0) ? 1 : (num1 * fact(num1 - 1)));
    }

    public static void Main()
    {
        Console.WriteLine("6! = {0}", fact(6));
        Console.WriteLine("What is your name?");
        Console.WriteLine("Hello, {0}", Console.ReadLine());
    }
}

This is part 3 of a series of posts on my Lisp compiler written in F#. Previous entries: Introduction, Parsing with fslex and fsyacc | Browse the full source of the compiler on GitHub

Thanks to fslex, fsyacc and the LispVal type, we've ended up with an expression tree that represents our program. To summarise, we've turned this:

(define (fact n) (if (= n 0) 1 (* n (fact (- n 1)))))
(Console.WriteLine "6! = {0}" (fact 6))
(Console.WriteLine "What is your name?")
(Console.WriteLine "Hello, {0}" (Console.ReadLine))

...into an F# data structure that looks like this:

[List
   [Atom "define"; List [Atom "fact"; Atom "n"];
    List
      [Atom "if"; List [Atom "="; Atom "n"; Number 0]; Number 1;
       List
         [Atom "*"; Atom "n";
          List [Atom "fact"; List [Atom "-"; Atom "n"; Number 1]]]]];
 List
   [Atom "Console.WriteLine"; String "6! = {0}"; List [Atom "fact"; Number 6]];
 List [Atom "Console.WriteLine"; String "What is your name?"];
 List
   [Atom "Console.WriteLine"; String "Hello, {0}";
    List [Atom "Console.ReadLine"]]]

We'd like to turn this data structure into actual IL, which we can execute. I'll assume some restrictions:

• We're going to compile, not interpret, and we're going to target .NET IL, not x86 machine code, LLVM, or anything else at this point
• Basic arithmetic (+, -, *, /) on integers
  (- n 1)
• Equality comparisons
  (= n 0)
• if statements
  (if (= n 0) a b)
• Call static .NET methods (no new operator and no instance methods)
  (Console.WriteLine "What is your name?")
• Define and call our own functions
  (define (fact n) (if (= n 0) 1 (* n (fact (- n 1)))))

What we'll do is:

1. Preprocess built-in forms such as arithmetic, define, if and lambda into specific nodes in the expression tree
2. Construct an instance of System.Reflection.Emit.ILGenerator. We could write an EXE or DLL file, but for experimentation, it's handy to target a DynamicMethod
3. Emit IL opcodes that implement the expression tree

First, a couple of pattern matching functions to recognise the built-in forms. Strictly speaking, we could write a code generator which recognises the built-in forms directly, but turning them into first-class expression tree nodes early on will hopefully make it easier to apply compiler optimisations, which I hope to add at some point.

CodeGenerator.fs

// Turn a LispVal into a function or variable name
let extractAtom = function
    | Atom a -> a
    | v -> raise <| Compiler(sprintf "expected atom, got %A" v)

// Note: insertPrimitives accepts a LispVal and returns a LispVal.
// The function keyword combines function declaration with pattern matching.
let rec insertPrimitives = 
    function
    // Convert arithmetic operators into ListPrimitive
    | List (Atom "+" :: args) -> ListPrimitive (Add, args |> List.map insertPrimitives)
    | List (Atom "-" :: args) -> ListPrimitive (Subtract, args |> List.map insertPrimitives)
    | List (Atom "*" :: args) -> ListPrimitive (Multiply, args |> List.map insertPrimitives)
    | List (Atom "/" :: args) -> ListPrimitive (Divide, args |> List.map insertPrimitives)
    | List (Atom "=" :: args) -> ListPrimitive (Equal, args |> List.map insertPrimitives)

    | List (Atom "define" :: args) ->
        match args with
        | [ Atom name; v ] -> 
            // Convert (define variableName value) into VariableDef
            VariableDef (name, insertPrimitives v)

        | [ List (Atom name :: names); body ] -> 
            // Convert (define functionName (x y z) value) into a VariableDef wrapping a LambdaDef
            // This represents a named static .NET method
            VariableDef (name, LambdaDef (names |> List.map extractAtom, insertPrimitives body))

        | _ -> 
            // Note: "raise <| Compiler message" is equivalent to C# "throw new CompilerException(message)"
            raise <| Compiler "expected define name value"

    | List (Atom "if" :: args) ->
        match args with
        | [ testValue; thenValue; elseValue ] -> 
            // Convert (if test then else) into IfPrimitive)
            IfPrimitive (insertPrimitives testValue, insertPrimitives thenValue, insertPrimitives elseValue)

        | _ -> 
            raise <| Compiler "expected three items for if"

    | List (Atom "lambda" :: args) ->
        match args with
        | [ List names; body ] -> 
            // Convert (lambda (x y z) value) into LambdaDef, without a VariableDef
            LambdaDef (names |> List.map extractAtom, insertPrimitives body)

        | _ -> 
            raise <| Compiler "expected lambda names body"

    | List l -> 
        // Apply insertPrimitives recursively on any function invokations
        l |> List.map insertPrimitives |> List

    | v -> v

The insertPrimitives function turns our parsed expression tree into this:

[VariableDef
   ("fact",
    LambdaDef
      (["n"],
       IfPrimitive
         (ListPrimitive (Equal,[Atom "n"; Number 0]),Number 1,
          ListPrimitive
            (Multiply,
             [Atom "n";
              List [Atom "fact"; ListPrimitive (Subtract,[Atom "n"; Number 1])]]))));
 List
   [Atom "Console.WriteLine"; String "6! = {0}"; List [Atom "fact"; Number 6]];
 List [Atom "Console.WriteLine"; String "What is your name?"];
 List
   [Atom "Console.WriteLine"; String "Hello, {0}";
    List [Atom "Console.ReadLine"]]]

We're going to write an F# function that emits IL for one line in our program, and looks like this:

let rec compile
    (generator : ILGenerator)
    (defineMethod : string -> Type -> Type list -> #MethodInfo * ILGenerator)
    (env : Map<string, LispVal>)
    (value : LispVal) 
    : (Map<string, LispVal>)

What this function signature tells us is:

• We have a recursive function called compile (by default, F# functions aren't allowed to call themselves, hence the rec keyword)
• It takes the following parameters:
  1. An ILGenerator, i.e. the target of the IL we're going to generate
  2. A function that accepts a string, a Type, a list of Type, and returns a tuple containing a MethodInfo (or a type derived from MethodInfo, hence the #) and another ILGenerator. This will be the callback that compile will call to create a new static method for lambda: the string is a function name, the Type is a return type, and the Type list is a list of parameter types.
  3. A Map of string to LispVal, i.e. the variables and functions defined by prior statements in the program
  4. A LispVal representing the statement to generate code for
• It returns Map<string, LispVal>, i.e. a copy of env, possibly with some new variables or functions added

I'll cover the details of the compile function itself in the next post. In this one I'd like to explain a couple of helper functions:

• typeOf, which returns the .NET Type denoted by a LispVal
• lambdaIdent, which retrieves a LambdaDef

We're using LambdaDef nodes not only to define our own functions (like fact in our example above, which calculates factorials), but also any .NET methods we call. typeOf and lambdaIdent call each other, so we have to define them together with F#'s and keyword in between them:

• typeOf needs to call lambdaIdent in order to determine the type returned by a function invocation
• lambdaIdent needs to call typeOf when it looks at the types of function arguments when deciding which overload of a .NET method to call

let rec typeOf (env : Map<string, LispVal>) = function
    | ArgRef _ -> typeof<int>
    | Atom a -> a |> ident env |> typeOf env
    | Bool _ -> typeof<bool>
    | IfPrimitive (_, thenValue, elseValue) ->
        match typeOf env thenValue with
        | t when t = typeOf env elseValue -> t
        | _ -> raise <| Compiler("expected 'then' and 'else' branches to have same type")

    | LambdaDef (_, body) -> typeOf env body
    | LambdaRef (methodBuilder, _, _) -> methodBuilder.ReturnType
    | List (Atom a :: args) -> a |> lambdaIdent args env |> typeOf env
    | List (fn :: _) -> raise <| Compiler(sprintf "can't invoke %A" fn)
    | List [ ] -> raise <| Compiler("can't compile empty list")
    | ListPrimitive _ -> typeof<int>
    | Number _ -> typeof<int>
    | String _ -> typeof<string>
    | VariableDef _ -> typeof<Void>
    | VariableRef local -> local.LocalType  

lambdaIdent is moderately complicated: it needs to take the name of a function and a list of arguments and determine the correct .NET overload to call. (Even though I'm trying to keep this compiler simple, we need overload resolution in order to call Console.WriteLine -- we can't write hello world without it.)

First, have we ourselves defined a function with the right name?

and lambdaIdent args env (a : string) =
    let envMatches = 
        maybe {
            let! v = Map.tryFind a env
            let! r =
                match v with
                | LambdaRef _ -> Some v
                | _ -> None
            return r
        } |> Option.to_list

Note: the maybe keyword isn't built into F#; we're using the F# equivalent of Haskell's Maybe monad, which a few other people have written about. Its purpose is to execute statements until one of them returns None; the result of the maybe block is determined by the return r at the bottom.

At this point, envMatches is a list of one or no LambdaRef nodes, taken from our environment. Next: attempting to parse the method name as Namespace.Class.Method. Again, note the use of maybe to simplify the code that deals with Option variables:

    let clrTypeAndMethodName = 
        maybe {
            let! (typeName, methodName) = 
                match a.LastIndexOf('.') with
                | -1 -> None
                | n -> Some (a.Substring(0, n), a.Substring(n + 1))

            let! clrType =
                referencedAssemblies
                |> List.map (fun assembly -> 
                    usingNamespaces 
                    |> List.map (fun usingNamespace -> (assembly, usingNamespace)))
                |> List.concat
                |> List.tryPick (fun (assembly, usingNamespace) -> option_of_nullable <| assembly.GetType(usingNamespace + "." + typeName))

            return (clrType, methodName)
        } 

referencedAssemblies and usingNamespaces are hard-coded equivalents to C#'s assembly references and using statements. Next: a list of all the .NET methods with the right name, albeit maybe without the right parameter list:

    let clrMatches =
        match clrTypeAndMethodName with
        | Some (clrType, methodName) -> 
            clrType.GetMethods(BindingFlags.Public ||| BindingFlags.Static) 
            |> List.of_array
            |> List.filter (fun m -> m.Name = methodName)
            |> List.map makeLambdaRef

        | None -> 
            [ ]

A function that determines whether a function's parameter list of compatible with a set of arguments. The isParamArray parameter indicates whether the .NET method has a variable parameter list (such as C#: void WriteLine(string format, params object[] args)).

    let argsMatchParameters = function
        | LambdaRef (_, isParamArray, parameterTypes) ->
            let rec argsMatchParameters' argTypes (parameterTypes : #Type list) =
                match argTypes, parameterTypes with
                | [ ], [ ] -> 
                    // No args and no parameters -> always OK
                    true

                | [ ], [ _ ] -> 
                    // No args and one parameter -> OK only for params array methods
                    isParamArray

                | [ ], _ ->
                    // No args and two or more parameters -> never OK
                    false

                | argType :: otherArgTypes, [ parameterType ] when isParamArray -> 
                    // One or more args and one parameter, in a params array method ->
                    //  OK if the types of the first arg and the params array are compatible,
                    //  and the rest of the args match the params array
                    parameterType.GetElementType().IsAssignableFrom(argType) 
                    && argsMatchParameters' otherArgTypes parameterTypes

                | argType :: otherArgTypes, parameterType :: otherParameterTypes -> 
                    // One or more args and one or more parameters -> 
                    //  OK if the types of the first arg and parameter are compatible, 
                    //  and the rest of the args match the rest of the parameters
                    parameterType.IsAssignableFrom(argType) 
                    && argsMatchParameters' otherArgTypes otherParameterTypes

                | _ :: _, [ ] -> 
                    // One or more args and no parameters -> never OK
                    false

            argsMatchParameters' (List.map (typeOf env) args) parameterTypes

        | _ -> false

Finally, a combined list of all candidates (both from the environment and from .NET), the method overloads whose parameters are compatible with our arguments, and the chosen overload itself. When given more than one compatible overload we pick the first one we've given. (The ECMA C# spec defines detailed rules for picking the most appropriate method overload, but we've ignoring those in our language.)

    let candidates = List.append envMatches clrMatches
    match candidates with
    | [ ] -> raise <| Compiler(sprintf "no method called %s" a)
    | _ -> ()

    let allMatches = List.filter argsMatchParameters candidates
    match allMatches with
    | [ ] -> raise <| Compiler(sprintf "no overload of %s is compatible with %A" a args)
    | firstMatch :: _ -> firstMatch

We're now able to take a method name (as a string) and a list of arguments (as LispVal nodes), and decide what to call, whether it's one of our own functions or a method in a .NET library. We've done a large chunk of the work ahead of the next post, in which we'll finally get round to generating some useful IL.