Tim Robinson

In my last Lisp compiler post, I talked about what I might need to do in order to support tail-recursive calls. I came to the conclusion that my compiler need to start describing the program as a graph of linked basic blocks.

To summarise, a basic block obeys two rules:

• It has a single entry point: the program isn't allowed to branch into the middle of the block
• It has a single exit point: the block always contains a single branch instruction, which appears at the end

For instance, here's a graph of a program that uses a recursive factorial function:

(define (factorial n)
  (if (= n 0) 
    1 
    (* n (factorial (- n 1)))))
(Console.WriteLine (factorial 6))

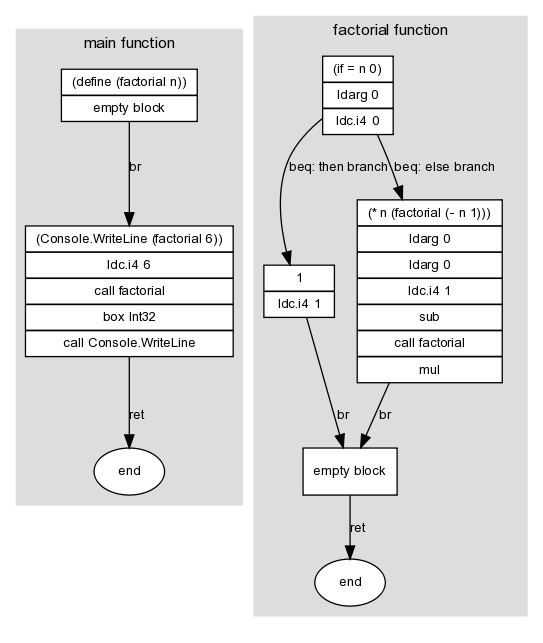
Here I've marked graph edges with a .NET branch instruction (in this case, br, beq or ret). These edges link the graph's nodes -- the basic blocks -- which is where the other instructions in the program appear. A block doesn't need to contain any instructions; for instance, the then and else branches of the if block both lead unconditionally to a single empty block, which in turn exits the function.

To represent the data structures in the graph I added three F# types to the compiler. All of them are immutable apart from ILBlock's Branch field, which I made mutable in order to allow circular references between blocks:

• ILOpCode: a discriminated union with one case for each IL opcode that can appear inside a block -- Add, Box of Type, Call of MethodInfo, etc. Note that call is not considered a branching opcode for these purposes, since it doesn't interrupt the control flow.
• ILBranchOpCode: a discriminated union with one case for each IL opcode that can appear at the end of a block - Beq of ILBlock * ILBlock, Br of ILBlock, Brtrue of ILBlock * ILBlock, NoBranch and Ret. The values for Beq and Brtrue specify both branch possibilities. Each ILBranchOpCode represents an edge in the graph.
• ILBlock: a record containing a list of IlOpCode and a mutable ILBranchOpCode field. Each ILBlock represents a basic block; that is, a node in the graph that can be linked by two or more ILBranchOpCodes.

These new data structures now allow me to split the code concerned with IL generation into two parts: a large function that turns the abstract syntax tree into a graph of basic blocks, and a class that takes this graph and uses it to emit IL code through an ILGenerator. (Actually there are two of these classes -- DynamicMethodTarget and MethodBuilderTarget -- because there is no common base between the two classes .NET provides to instantiate an ILGenerator.)

I won't list out the code in full, since I've submitted it to GitHub (CodeGeneration.fs) and because it's got broadly the same structure as the last time I posted it. The difference is that most of the work is performed by a makeBlock function:

val makeBlock : IILTarget -> Map<string, LispVal> -> LispVal -> Map<string, LispVal> * ILBlock * ILBlock

The purpose of this function is to:

• Accept an IILTarget, an interface capable of defining new methods and local variables; a map, which contains the environment at this point in the program; and a LispVal, which represents one line of code
• Return a new environment, which could be modified version of the one passed in; and two ILBlock instances, which represent the head and tail of a new subgraph

Normally makeBlock will construct only a single block, in which case both the same block object will be returned twice. An if form is more complicated, in that it consists of a diamond shape: the block that contains the code for the test can branch to either the then or the else block, both of which eventually branch back to the same location so that the program can continue. When generating code for an if, makeBlock will return the blocks at the top and bottom of the diamond, ready to be linked together with the rest of the program. (The edges between the then and else blocks are already added.)

Now the the clever part: because we've got the program's structure and code as a graph in memory, we can do some more interesting optimisations. The process of turning this graph into IL goes as follows:

1. Iterate through the graph and assign a IL label to each block. With a depth-first recursive search we have to be careful not to get stuck in a circular reference: to avoid this we keep track of blocks we've already encountered.
2. Iterate through the graph again: generate instructions for each block, followed by an instruction for the block's branch

Take a look at the diagram at the top of this post. Because the diagram doesn't assume a particular ordering of the instructions in memory -- for instance, it doesn't specify whether then or else comes first -- some of its branch instructions are redundant. To generate somewhat sensible IL we have to do some basic optimisations in step (2):

• Case A: If step (1) put two blocks next to each other in memory, we don't need to insert a br instruction between them. Recall that br is an unconditional jump instruction; by leaving it out, we cause the program to fall through from one block to the next.
• Cases B and C: Likewise, use the ordering of the blocks to drop one of the targets of beq and replace it with a fall through
• Case D: If block branches to its target using br, and its target contains no instructions and ends in ret, insert a ret instruction directly

These rules give us a nice opportunity to use pattern matching -- note how the structure of the code is similar to my explanation above:

// Given a list of blocks:
// - branch is the ILBranchOpCode of the first block
// - otherBlocks is a list containing the rest of the blocks
match branch, otherBlocks with
| Br target, next :: _ 
    when target = next -> // Case A
    ()
| Beq (equalTarget, notEqualTarget), next :: _ 
    when equalTarget = next -> // Case B
    generator.Emit(OpCodes.Bne_Un, labels.[notEqualTarget])
| Beq (equalTarget, notEqualTarget), next :: _ 
    when notEqualTarget = next -> // Case C
    generator.Emit(OpCodes.Beq, labels.[equalTarget])
| Br { Instructions = [ ]; Branch = Ret }, _-> // Case D
    generator.Emit(OpCodes.Ret)
| branchOpCode, _ ->    // None of the above apply
    emitBranch labels branchOpCode

Finally -- and here's what I've been building up to with these last couple of posts -- we can implement tail call recursion, using the tail.call prefix. Our graph data structures allow us to literally look for the situation that the IL spec requires: a call instruction immediately followed by ret. In our case, this happens when a block's branch is Ret, and the last instruction of that block is Call:

let rec emitInstructions block = 
    let isRetBlock =
        // A slight hack: due to the above optimisations,
        //  there's a couple of ways of emitting a Ret
        match block with
        | { Branch = Ret } -> true
        | { Branch = Br {
            Instructions = [ ]; 
            Branch = Ret } } -> true
        | _ -> false
    function
    | [ Call _ as instruction ] when isRetBlock ->
        generator.Emit(OpCodes.Tailcall)
        emitInstruction instruction
    | instruction :: otherInstructions ->
        emitInstruction instruction
        emitInstructions block otherInstructions
    | [ ] ->
        ()

By reorganising my compiler to support tail recursion I've learned that:

• Changing your data structures (in this case, implementing a control flow graph) can often make a previously difficult algorithm (tail call detection) straightforward
• If you haven't got any unit tests, you're not refactoring, you're just changing stuff. I've now written unit tests for the main features supported by the compiler. As an aside, I think NUnit tests written in F# look nicer than their C# equivalents, although I was slightly disappointed that NUnit made me write a class with instance methods, whereas it would have been neater to have some functions for test cases defined directly inside an F# module.
• Writing a blog post on a topic before attempting it is a great way to get your thoughts clear in your head before starting

What I might look at next is some more sophisticated algorithms over the control flow graph. Once you have a graph you make available a whole field of algorithms to use on your data. I haven't looked at it yet in detail, but I like Steve Horsfield's data structure for modelling directional graphs.